马丁格尔博彩系统是什么?
有些玩家喜欢资金管理策略,但人们相信这些策略是否可靠?Joseph Buchdahl 调查了 Martingale 博彩系统,以确定这些回报是否真的值得风险。
一些博彩平台会员和情报商使用资金管理策略,即在投注失败后追加注码以试图翻本。
支持者经常将其视为一种故障安全策略,即早晚要赢一次,然后赚取所有以前亏的钱。
如果你是一个更聪明的人,你可能已经意识到博彩的缺陷:没有什么是不可避免的,如果有的话,那就不是博彩。有些玩家忽视这个缺陷的原因是几个诱导式的错误:过度自信(他们一定会赢),低估了连败的可能性。这种博彩资金管理在过去被称为马丁格尔系统。
马丁格尔策略
马丁格尔投注计划来自博彩业,尤其是轮盘赌。在轮盘上玩一种非常流行的游戏是赌黑色和红色。在这个博彩平台游戏中,玩家必须选择球转到最终落在红色数字上还是黑色数字上。
无论结果的赔率是多少,赌场的优势都不重要。马丁格尔的基本策略是每次赌输后将注码加倍,然后每次赌赢后回到起始注码(或基线)。然而,这个公式也可以用于任何投注赔率:
马丁格尔加码率等于赔率/(赔率- 1)。
例如,如果投注赔率为 3.00,加码率应该为 1.5。
如以下轮盘转动结果所揭示的那样,以这种方式,在每次获胜结果后收回以前的损失,外加最初的目标利润。
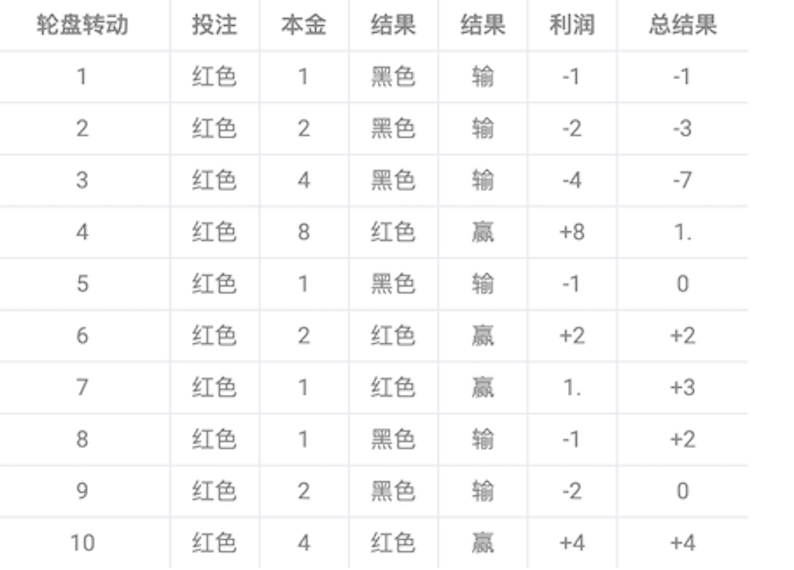
马丁格尔改变了风险,而非数学期望
Stuart Holland 在 2001 年出版的电子书《成功注金策略》(Successful Staking Strategies)中提供了一个简单而又极其有效的证明,解释了为什么马丁格尔没有空手套白狼。
考虑一下前面列出的三个轮盘转动。黑色连输 3 次仅代表 8 种可能结果中的 1 种,每个结果的可能性都与其他任何一次相同。
下表显示了这八种排列组合的利润期望值(R 为红色,B 为黑色),不考虑赌场优势(绿色零)。要计算任何结果的期望值,只需将实际收益和损失乘以其发生概率。
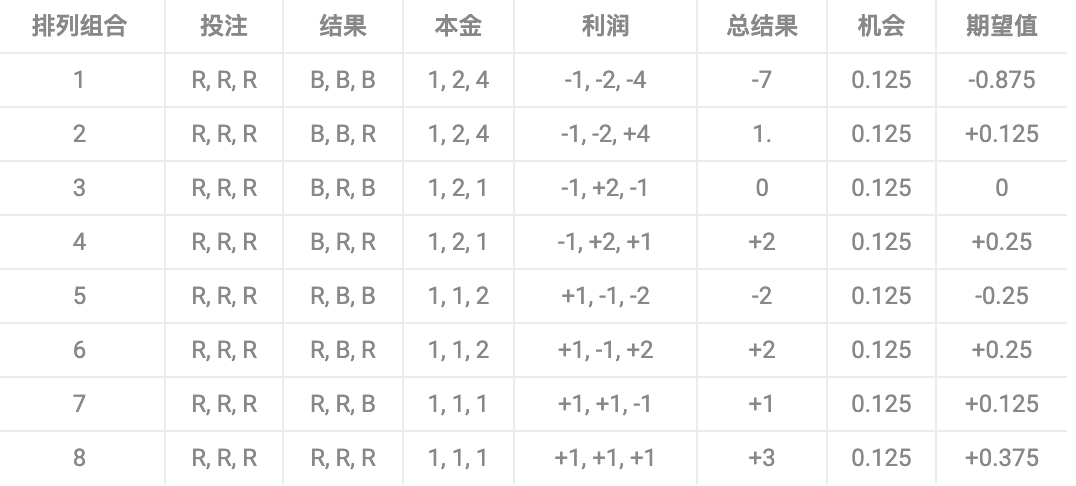
将这八种排列组合的单独期望相加,得到该策略的总期望值,该值为零。因此,对于公平的轮盘赌来说,我们可以期望不赔不赚。当然,现实的轮盘赌不是公平的;游乐场的一次黑红游戏带来的期望值为负,因此很多次游戏的总和也是负数。对平注(其中所有本金相同)的类似分析得到完全相同的结果:总期望值为零。
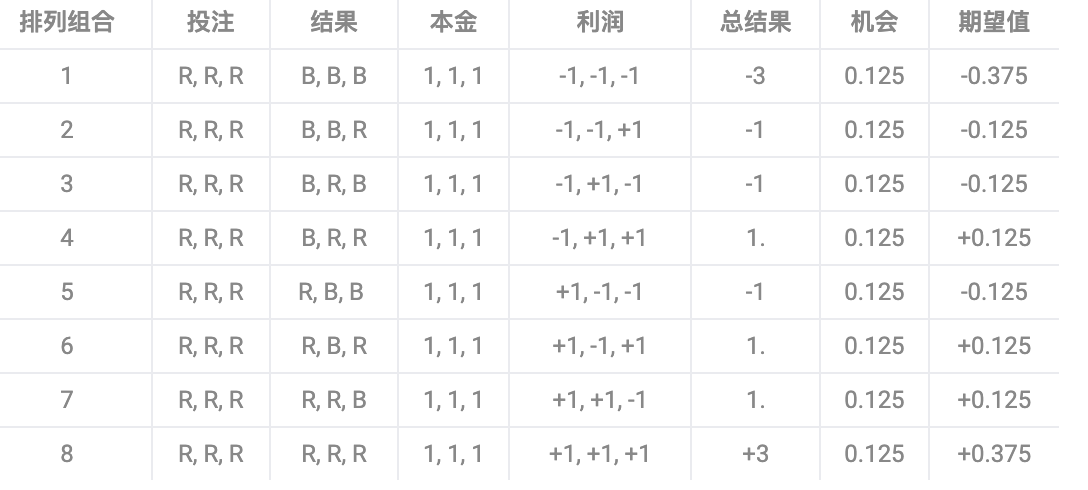
来看看这两台赌桌。马丁格尔的策略相对于平注策略使我们可以盈利的预期次数增加,在本例中从 4 提高到 5,但遗憾的是,这是以一次亏损为代价的。马丁格尔真正实现的只是改变了风险的分布。相对于平注的对等结果,多换取一次有正期望值的结果,需要另一次有负期望值的结果。这就是这种博彩策略与固有风险相关的原因。
使用马丁格尔策略
在体育博彩中,马丁格尔加码法看起来似乎可以让玩家获利,即使他们无法确定正期望值,因为每次获胜都会让他们以前的损失得到补偿,每次小赚一笔。然而,前面的分析可能会说服你,马丁格尔加码法不仅在数学上存在缺陷,而且它本身就有很大的风险,因为每次连输十把一对一的投注将需要第11把注码1,024个单位来赢1个单位。
根据你开始注码的大小,可以想见这可能超过博彩公司允许的上限。同样,从你剩余的资金中可能拿不出这么多钱来。
低估了输下去的可能
在一对一投注中连输十把的可能性有多大?单独来看,计算结果的数学方法很简单。如果每次独立投注有 50%(或 0.5)的概率输,那么连输 10 次的概率是 0.5×10 = 0.0977%。
这种低概率吓坏了很多人,使他们相信马丁格尔是一种相对安全的选择。然而,在一系列更大的投注过程中,发生这种连输的可能性又是何种情况?
虽然这种计算的数学方法要复杂得多,但我们可以直觉地确定,由于发生的机会要多得多,这种可能性要比前面提到的单独一次连输的百分比要高得多。很幸运,有一种非常有用的方法可以估算很长一串投注中可能预计的最长连输时间。
S_L 是 Ln(N)/(Ln(O_L) 的平方。
S_L是预计的最大连输,N是投注总次数,Ln是自然对数(可以用任何科学计算器计算),O_L是输掉单次投注的赔率,可以由取胜赔率或投注赔率O_W计算:
O_L = O_W/(O_W-1)
例如,在公平赔率为 2.00 的一系列 1000 次投注中,我们通常会预期至少有 10 次连输。正如我们已经看到的那样,这种注码意味着下一次押下去的需要比第一次大 1024 倍。因此,为了合理应对这种连输期望值,您的资金和基线注码的比例将相应进行调整。您投注序列拉得越长,基线注码占到您的资金的比例就越小。
对于一系列 1000 次一对一投注,您的资金应该至少比基线注金大 1000 倍。这意味着,要么基线注码和取胜后利润是如此之小,几乎不值得遵循这样的策略,要么您将面临巨大的风险。
破产风险
在 2003 年出版的一本书《锁定赔率体育博彩:统计预测和风险管理》(Fixed Odds Sports Betting: Statistical Forecasting and Risk Management)中,我对 Martingale 策略进行了测试,该策略的平均取胜期望是 0.5,即 2.00 的赔率。
假设这种赔率是合理的,对于初始资金1%的基线注码,最后破产的可能性是53%。对于平注策略来说,这个百分比太小了,基本上是零。马丁格尔策略的破产风险为 65% 和 78%,如果博彩公司比玩家占利润的比例为 10% 和 5%。
即使在游戏中保持优势的情况下,风险仍然相当大。以 5% 的优势,破产率仍然高达 38%。当玩家通过他们的预测技巧锁定正预期价值时,很奇怪为什么他们没有赢就想着要输。
一种幻觉
从理论上讲,马丁格尔策略可以成为一种成功的策略,只要拥有无穷的财富、无数次投注、无限长的时间和任何博彩平台公司都来者不拒。当然,除非是这样,否则就无法增加无穷的财富。如果有人已经拥有无穷的财富并且可以打败赔率,那么马丁格尔策略提供了笃定可能的方法让财富全部灰飞烟灭。
马丁格尔策略显而易见的翻本能力只是幻觉,而且在这种情况下非常危险。